No se preocupe por sus dificultades en las matemáticas. Yo puedo asegurarle que las mías son todavía mayores.
John Locke

La Topología es la rama de las matemáticas dedicada al estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. (Ian Stewart)

En topología es muy importante el Teorema de la Curva de Jordan que dice que: toda curva cerrada simple divide al plano en dos conjuntos disjuntos que tienen a la curva como frontera común. Uno de estos conjuntos está acotado  y se le llama el interior de la curva, y el otro no es acotado y se le llama exterior. Camille Jordan

El teorema fue demostrado por Oswald Veblen en 1905.

Este teorema extraordinario es, a pesar de lo sencillo y simple del enunciado,  de difícil demostración. Cabe destacar a su vez, que no es válido en cualquier superficie, por ejemplo es válido en el plano y en la esfera pero no es válido en un toroide.

Una curva  cerrada simple del plano es una curva unida por sus extremos y que no se cruza a si misma. Se la llama curva de Jordan.

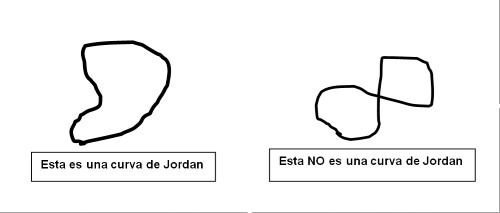
  Como vimos la curva de Jordan determina dos regiones: un adentro y un afuera.

  
¿Dónde está el punto A, en el interior o en el exterior de la curva?

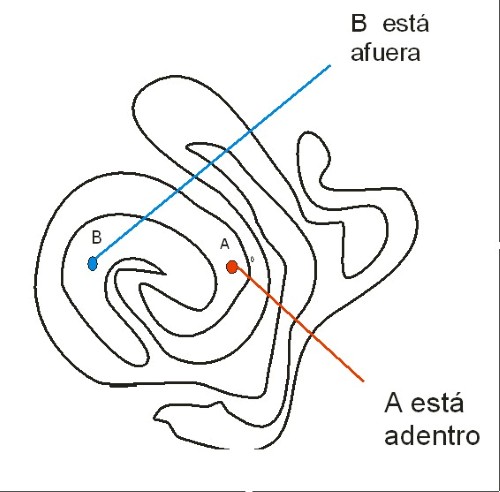
Pero la curva puede complicarse y como se muestra en las figuras de abajo que fueron tomadas de la Web, puede ser difícil a simple vista determinar donde está el punto A. ¿Está adentro o está afuera?


 
 
Tendríamos que agarrar un lápiz y seguir el laberinto para saber donde está. Pero,… existe un procedimiento que permite saber donde está el punto A. Se traza una semirrecta desde el punto hasta el exterior. Si la semirrecta corta a la curva un número PAR de veces, el punto está en el exterior; si la semirrecta corta a la curva un número IMPAR de veces el punto está en el interior.

Ver ejemplo a continuación:

 

Y ahora vamos al siguiente juego:
En la figura siguiente no se puede seguir con el lápiz ni tampoco aplicar el procedimiento explicado, dado que solo se ve una pequeña parta de la curva, puesto que a los costados, se encuentra tapada por los cuatro rectángulos.

  

Entonces, sabiendo que el punto B está afuera ¿Dónde está el punto A, adentro o afuera?

SOLUCIÓN

Si se traza un segmento de recta que una los puntos A y B, vemos que corta a la curva un número IMPAR de veces, eso significa que están en distintas regiones. Si el número de cortes es PAR, quiere decir que están en la misma región.